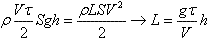Олимпиадные задания 11 класс с ответами по физике
Олимпиадные задания 11 класс с ответами по физике
Олимпиадные задания с ответами по физике 11 класс
9 класс 10 класс
Две одинаковые шайбы массы M каждая скреплены невесомой пружиной и лежат на плоскости. Коэффициент трения между шайбами и плоскостью равен k, а трение пружины о плоскость отсутствует. Плоскость начинают медленно наклонять так, что пружина сохраняет горизонтальное расположение. При каком угле наклона плоскости к горизонту шайбы начнут скользить по ней? Первоначальная сила натяжения пружины T0. На гладкой горизонтальной поверхности лежит мишень массы 9 кг. С интервалом в t=1 с в нее попадают и застревают 4 пули, первая из которых летит с юга, вторая - с запада, третья - с севера и четвертая с востока. На сколько и в какую сторону сместится в итоге мишень? Масса каждой пули 9г, скорость v= 200 м/с. Вокруг звезды "Икс" вращаются две планеты массы M = 6 1024 кг каждая, состоящие из несжимаемой жидкости плотности 1000кг/м3. Одна из планет электрически нейтральна, а по объему второй равномерно распределен электрический заряд Q =10000 Кл. Найдите отношение давлений в центре планет. Наблюдая Землю, марсианский астроном видит, что Солнцем освещена ровно половина видимого диска. Найдите расстояние от Марса до Земли, если известно, что Земля и Марс находятся на расстоянии 147 и 245 миллионов километров от Солнца. Снаряд, выпущенный со скоростью v0 из пушки, находящейся на поверхности земли, разорвался на два одинаковых осколка. Один из них полетел вертикально вверх, а второй - горизонтально, оба со скоростями v0/2. На какой высоте произошел взрыв? Внутри полого шара массы М с внутренним радиусом 5 см находится маленький шарик массы М/10. Снаружи на большой шар налетает еще один маленький шарик массы М/10 со скоростью 2 м/с. Найдите период колебаний малого шара внутри большого, которые возникнут в итоге. Все удары центральные и абсолютно упругие. Опыт проводится в невесомости. Внутри сосуда объема V помещена резиновая оболочка объема V/4. И сосуд, и оболочка заполнены идеальным газом. В начальном состоянии температура газа T0 и оболочка не растянута. Когда газ внутри оболочки нагрели до температуры T1, сохраняя температуру остального газа неизменной, оболочка раздулась, и ее объем увеличился вдвое. До какой температуры нужно охладить газ в сосуде, поддерживая температуру T0 внутри оболочки, чтобы она раздулась до тех же размеров? Считать, что упругие свойства оболочки не зависят от температуры. Из вершин правильного шестиугольника со стороной 1 м одновременно пускают по направлению к центру шесть одинаковых заряженных частиц. Начальная скорость частиц 1 м/с. Когда расстояние между частицами уменьшилось в два раза, то скорость каждой также уменьшилась вдвое.
До какого минимального расстояния сблизятся частицы?
Задачи олимпиады по физике 11 класс
Вариант №1
(5 баллов) Два человека одновременно вступают на эскалатор с противоположных сторон и движутся навстречу друг другу с одинаковыми скоростями относительно эскалатора V=2 м/с. На каком расстоянии от входа на эскалатор они встретятся? Длина эскалатора L=100 м, его скорость U=1,5 м/с.
(10 баллов) Вне изолированной удаленной от земли и от других предметов металлической незаряженной сферы радиуса R на расстоянии r от ее центра находится точечный заряд q. Каков потенциал сферы? Ответ обосновать.
(10 баллов) Электрический элемент с вольтамперной характеристикой I=AU2 (A=const, U>0) подключили к источнику ЭДС. Найти напряжение на элементе, если ЭДС источника равна ε, а внутреннее сопротивление источника — r.
(10 баллов) «Электромагнитная пушка» представляет из себя две параллельные проводящие шины, замкнутые перемычкой-снарядом, которая может свободно перемещаться вдоль шин. Вся конструкция расположена в однородном магнитном поле с индукцией В, линии индукции которого ориентированы перпендикулярно плоскости шин. Выстрел происходит при пропускании электрического тока через шины. Найти скорость снаряда, вылетающего из такой пушки при горизонтальной ее ориентации, если длина шин L, масса снаряда-перемычки m, расстояние между шинами d, сила тока в шинах I.
(10 баллов) В стальном баллоне находится ν1=0,1 моля водорода и ν2=0,1 моля кислорода при температуре t=27oС. Смесь газов в баллоне поджигают и, после того как реакция закончится, давление внутри баллона увеличивается в 3 раза. Какая температура будет внутри баллона после реакции?
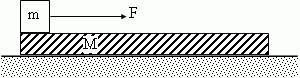 (10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Через какое время брусок соскользнет с доски? (10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Через какое время брусок соскользнет с доски?
(15 баллов) На горизонтальной поверхности лежит шланг, заполненный водой, оба отверстия которого закрыты пробками. Один конец шланга подняли на высоту h (второй остался лежать на поверхности) и одновременно вынули обе пробки. Спустя малый промежуток времени t вода в шланге приобрела скорость V. Найти длину шланга.
Вариант №2
(5 баллов) Расстояние от пункта А до пункта В, расположенных на берегу реки, катер проходит за время t1=3 ч, обратный путь у катера занимает t2=6 ч. Какое время потребуется катеру, чтобы пройти расстояние от А до В при выключенном моторе? Скорость катера относительно воды постоянна.
(10 баллов) Металлический шар радиуса R1, удаленный от земли и от других проводников, имеет потенциал φ1. Его окружают сферической проводящей оболочкой радиуса R2. Чему будет равен потенциал шара, если заземлить оболочку? Ответ обосновать.
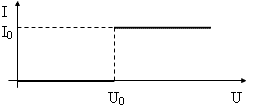
(10 баллов) Вольт-амперная характеристика некоторого нелинейного электрического элемента имеет вид, показанный на рисунке. Его включают в сеть, напряжение в которой равномерно меняется от нуля до значения 2U0 за время t0. Чему равна работа источника тока за это время?
(10 баллов) Тонкий стержень длины l и массы m подвесили за концы на двух одинаковых легких нерастяжимых проводящих нитях длиной L в однородном вертикальном магнитном поле с индукцией В так, что его ось горизонтальна, а нити вертикальны. Затем через нити пропустили заряд q столь быстро, что стержень практически не сместился от положения равновесия. Найти максимальный угол отклонения нитей подвеса от вертикали.
(10 баллов) Имеется смесь двух одноатомных газов с молярными массами μ1 и μ2. При температуре газа Т0 и давлении Р0 плотность смеси равняется ρ. Какова концентрация n1 атомов первого газа в смеси?

(10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К доске приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Через какое время брусок упадет с доски?
(15 баллов) На горизонтальной поверхности лежит шланг, заполненный водой, оба отверстия которого закрыты пробками. Один конец шланга подняли на высоту h (второй остался лежать на поверхности) и одновременно вынули обе пробки. Спустя малый промежуток времени τ вода в шланге приобрела скорость V. Найти длину шланга.
Вариант №3
(5 баллов) По двум параллельным путям равномерно движутся два поезда: товарный, длина которого L1=630 м и скорость V1=48 км/час, и пассажирский длиной L2=120 м со скоростью V2=102 км/час. Какова относительная скорость движения поездов, если они движутся: а) в одном направлении; б) в противоположных направлениях? В течение какого времени один поезд проходит относительно другого?
(10 баллов) Металлический шар радиуса R соединен тонкой длинной проволокой с землей. На расстоянии r>R от центра шара помещают точечный заряд q. Какой заряд Q приобретает шар? Влияние проволоки на электрическое поле не учитывать. Ответ обосновать.
(10 баллов) Электрический элемент с вольтамперной характеристикой I=AU2 (A=const, U>0) подключили к источнику ЭДС. Найти ток в цепи, если ЭДС источника равна ε, а внутреннее сопротивление источника — r.
(10 баллов) «Электромагнитная пушка» представляет из себя две параллельные проводящие шины, замкнутые перемычкой-снарядом, которая может свободно перемещаться вдоль шин. Вся конструкция расположена в однородном магнитном поле, линии индукции которого ориентированы перпендикулярно плоскости шин. Выстрел происходит при пропускании электрического тока через шины. Найти индукцию магнитного поля, если длина шин L, максимально возможная высота подъема снаряда, вылетающего из такой пушки, равна h (h>>L), масса снаряда-перемычки m, расстояние между шинами d, сила тока в шинах I.
(10 баллов) В стальном баллоне находится ν1=2 моля водорода и ν2=4 моля кислорода при давлении Р0. Смесь газов в баллоне поджигают. Каково будет давление в баллоне, когда реакция закончится, и смесь газов охладится до первоначальной температуры?
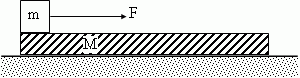 (10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Какую скорость будет иметь брусок в момент соскальзывания с доски? (10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Какую скорость будет иметь брусок в момент соскальзывания с доски?
(15 баллов) На горизонтальной поверхности лежит шланг, заполненный водой, оба отверстия которого закрыты пробками. Один конец шланга подняли на высоту h (второй остался лежать на поверхности) и одновременно вынули обе пробки. Спустя малый промежуток времени τ вода в шланге приобрела скорость V. Найти длину шланга.
Вариант №4
(5 баллов) Скорость велосипедиста равна 10 м/с, а скорость встречного ветра — 4 м/с. Какова скорость ветра относительно велосипедиста? Какой была бы скорость ветра относительно него, если бы ветер был попутный?
(10 баллов) Металлический шар радиуса R1, удаленный от земли и от других проводников, имеет потенциал φ1. Его окружают сферической проводящей оболочкой радиуса R2. Каким станет потенциал шара после того, как он на некоторое время будет соединен с оболочкой? Ответ обосновать.
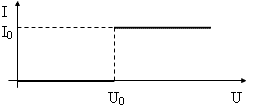
(10 баллов) Вольт-амперная характеристика некоторого нелинейного электрического элемента (НЭ) имеет вид, показанный на рисунке. Совместно с резистором, сопротивление которого равно R, его подключают к источнику тока (соединение НЭ и резистора последовательное). Напряжение на клеммах источника меняется во времени по закону U(t)=At (A=const). За какое время tx на резисторе R выделится количество теплоты Q?
(10 баллов) Тонкий стержень длины L и массы m покоится на горизонтальной плоскости в однородном горизонтальном магнитном поле с индукцией В (стержень перпендикулярен линиям индукции). Затем через стержень за очень малый промежуток времени пропустили электрический заряд (соединительные провода гибкие и невесомые). В результате этого стержень «подпрыгнул» над плоскостью на высоту h. Найти величину заряда q, пропущенного через стержень.
(10 баллов) Лазерные трубки одинакового объема V0 заполняются смесью гелия и неона. Причем количественное (молярное) отношении He:Ne должно быть равно 5:1 при общем давлении смеси газов Р0. Имеются баллоны с этими газами одинакового объема V=100V0. В баллоне с гелием давление Р1=10Р0, в баллоне с неоном давление Р2=4Р1. Какое число трубок можно заполнить? Температура газов одинакова и постоянна.

(10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К доске приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Какую скорость будет иметь брусок в момент соскальзывания с доски?
(15 баллов) На горизонтальной поверхности лежит шланг, заполненный водой, оба отверстия которого закрыты пробками. Один конец шланга подняли на высоту h (второй остался лежать на поверхности) и одновременно вынули обе пробки. Спустя малый промежуток времени t вода в шланге приобрела скорость V. Найти длину шланга.
Решение задач по физике 11 класс
Вариант №1
Время движения до встречи 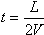 . Искомое расстояние . Искомое расстояние 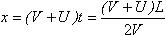 =87,5 м. =87,5 м.
Потенциал в центре сферы (точке О) равен потенциалу самой сферы (поле внутри сферы отсутствует). Этот потенциал складывается из потенциала заряда q и потенциала зарядов, индуцированных на поверхности сферы. Т.к. суммарный индуцированный заряд равен 0 и поверхность сферы равноудалена от точки О, то потенциал индуцированных зарядов в точке О равен 0. Т.е. потенциал точки О (он же потенциал сферы) определяется только зарядом q. Следовательно,
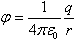
U+Ir = ε → U+ArU2 = ε → ArU2 + U – ε = 0 → U1,2 =  Т.к. U>0, то U = Т.к. U>0, то U = 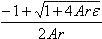
Сила, действующая на перемычку
F = IdB → FL = mV2 / 2 → 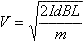 . .
Схема реакции 2H2 + O2 = 2H2O → в реакцию вступает только 0,05 моля кислорода. До реакции в баллоне количество вещества ν1 = 0,2, после реакции количество вещества в баллоне (кислород + вода) ν2 = 0,15
До реакции P1V = ν1RT1 , после реакции P2V = ν2RT2 →
T2 / T 1 = P2ν1 / P1ν2 = 4 → Т2 = 4Т1 = 1200 К.
F – μmg = maбр → абр = F / m – μg
μmg = Mад → ад = (m / M) μg.
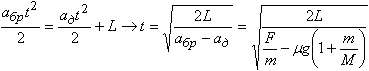
В течение короткого времени τ вода в шланге двигалась равноускоренно с ускорением a = V / τ. Из шланга вытекла вода, объем которой 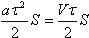 , где S — площадь сечения шланга. , где S — площадь сечения шланга.
Из закона сохранения энергии (ρ — плотность воды, L — длина шланга)

Вариант №2
V — скорость катера относительно воды, U — скорость течения, L — расстояние от А до В.
V + U = L / t1, V – U = L / t2, откуда U = 1/2 (L / t1 – L / t2). Искомое время 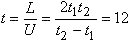 ч. ч.
Потенциал оболочки φ0 складывается из потенциала в поле шара, несущего на себе заряд Q1, и потенциала, обусловленного наведенным на ней зарядом Q2: 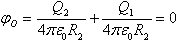 (оболочка заземлена), откуда Q2 = –Q1. Потенциал шара будет складываться из потенциала φ1, обусловленного его собственным зарядом, и потенциала φ2, обусловленного зарядом оболочки Q2 = –Q1: φ = φ1 + φ2 = φ1 (R2 – R1) / R2. (оболочка заземлена), откуда Q2 = –Q1. Потенциал шара будет складываться из потенциала φ1, обусловленного его собственным зарядом, и потенциала φ2, обусловленного зарядом оболочки Q2 = –Q1: φ = φ1 + φ2 = φ1 (R2 – R1) / R2.
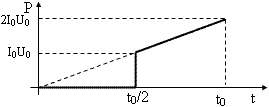
Мощность источника P=IU. Исходя из заданной ВАХ, ф-я P(t) имеет вид (см. рис.). Искомая работа равна площади трапеции 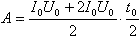 . .
Пусть t — время пропускания тока через стержень. В течение времени t на стержень действует горизонтальная сила (сила Ампера) 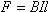 . Импульс этой силы равен импульсу, приобретенному стержнем, (V — скорость стержня в момент t). Отсюда . Импульс этой силы равен импульсу, приобретенному стержнем, (V — скорость стержня в момент t). Отсюда  . Из закона сохранения энергии . Из закона сохранения энергии 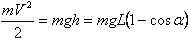 , откуда , откуда 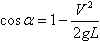 → →  . .
Р1 и Р2 — парциальные давления газов 1 и 2 в смеси, m1 и m2 — массы газов, ρ1 и ρ2 — их плотности, V — объем сосуда.
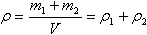 , P0 = P1 + P2. Из уравнения Клапейрона-Менделеева для давлений P1 и P2 имеем , P0 = P1 + P2. Из уравнения Клапейрона-Менделеева для давлений P1 и P2 имеем 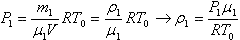 и и  . .
Тогда .
Из основного уравнения МКТ 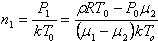 . .
aдM = F – Fmp, aбрm = Fmp и Fmp = μmg. Отсюда и aбр = μg. К моменту соскальзывания бруска t выполняется условие 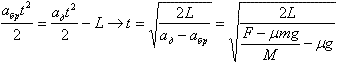 . .
В течение короткого времени τ вода в шланге двигалась равноускоренно с ускорением a = V / τ. Из шланга вытекла вода, объем которой 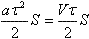 , где S — площадь сечения шланга. , где S — площадь сечения шланга.
Из закона сохранения энергии (ρ — плотность воды, L — длина шланга)
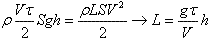
Вариант №3
 , , 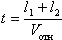
а) Vотн=V2–V1=54 км/ч, t=50 c. б) Vотн=V2+V2, t=18 с. Потенциал шара и всех точек (в том числе и точки О — его центра) внутри шара равен нулю. Потенциал точки О φ0 складывается из потенциалов, создаваемых зарядами q и Q: φ0 = φQ + φq. Т.к. элементарные заряды, составляющие заряд Q, распределенный по поверхности шара, равноудалены от его центра, то 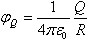 . Тогда . Отсюда . Тогда . Отсюда 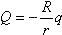 . U + Ir = ε из условия . U + Ir = ε из условия 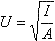 , тогда , тогда
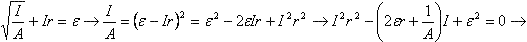
. Т.к. по условию U>0 то I<ε/r, следовательно, знак «+» исключаем. Окончательно
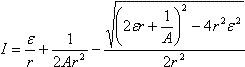 . Сила, действующая на перемычку . Сила, действующая на перемычку
F = IdB → FL = IdBL = mV2/2 = mgh → B = mgh / IdL. Схема реакции 2H2 + O2 = 2H2O. После реакции в баллоне ν1' = 3 моля килорода и ν2' = 2 моля воды. До реакции P0V = (ν1+ν2)RT0, после реакции PV = (ν1'+ν2')RT0 →
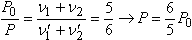 . F – μmg = maбр → абр = F/m – μg . F – μmg = maбр → абр = F/m – μg
μmg = Mад → ад = M/m * μg
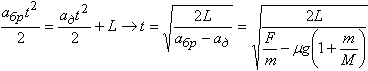 → V = aбрt. В течение короткого времени τ вода в шланге двигалась равноускоренно с ускорением a = V/τ. Из шланга вытекла вода, объем которой → V = aбрt. В течение короткого времени τ вода в шланге двигалась равноускоренно с ускорением a = V/τ. Из шланга вытекла вода, объем которой 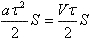 , где S — площадь сечения шланга. , где S — площадь сечения шланга.
Из закона сохранения энергии (ρ — плотность воды, L — длина шланга)
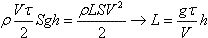
Вариант №4
В случае встречного ветра Vr = V1 + V2 = 14 m/c.
В случае попутного ветра Vr = V 1 – V2 = 6 m/c. Заряд шара до соединения с оболочкой равен Q1 = 4πε0R1φ1.
После соединения с оболочкой весь заряд перетечет на нее, а потенциал шара станет равным потенциалу оболочки: 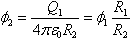 . Ток, равный I0, начинает течь в момент t0 = U0 / A. При этом выделившееся тепло равно Q = I02R (t–t0). Отсюда . Ток, равный I0, начинает течь в момент t0 = U0 / A. При этом выделившееся тепло равно Q = I02R (t–t0). Отсюда 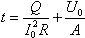 . Импульс, приобретенный стержнем равен mV = FΔt = BliΔt = qBL. С другой стороны . Импульс, приобретенный стержнем равен mV = FΔt = BliΔt = qBL. С другой стороны 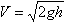 . Отсюда . Отсюда 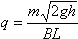 . PV = νRT. При V=const и T=const, P~ν. . PV = νRT. При V=const и T=const, P~ν.
P0=P10+P20, где P10 и P20 — парциальные давление гелия и неона.
По условию в трубке должно быть P10:P20 = 5:1, а в баллонах мы имеем P1:P2 = 1:4, следовательно, число заполненных трубок определяется только количеством гелия.
ν1 — количество гелия в баллоне, ν10 — количество гелия в одной трубке.
Тогда количество трубок (первое приближение) 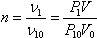 . .
Используя данные условия 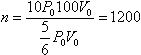 . .
Надо учесть, что после падения давления газа в баллоне до величины Р10 газ в трубку не пойдет, отсюда, уточненное количество трубок. aдM = F – Fmp, aбрm = Fтр и Fтр = μmg. Отсюда 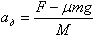 и aбр = μg. К моменту соскальзывания бруска t выполняется условие и aбр = μg. К моменту соскальзывания бруска t выполняется условие
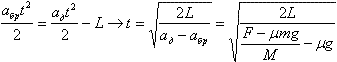 . .
Скорость бруска в момент соскальзывания равна
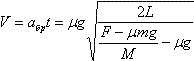 . В течение короткого времени τ вода в шланге двигалась равноускоренно с ускорением a = V / τ. Из шланга вытекла вода, объем которой . В течение короткого времени τ вода в шланге двигалась равноускоренно с ускорением a = V / τ. Из шланга вытекла вода, объем которой 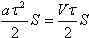 , где S — площадь сечения шланга. , где S — площадь сечения шланга.
Из закона сохранения энергии (ρ — плотность воды, L — длина шланга)
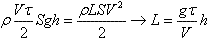
|
|
 Олимпиадные задания по физике
Олимпиадные задания по физике (10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Через какое время брусок соскользнет с доски?
(10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Через какое время брусок соскользнет с доски? 

 (10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Какую скорость будет иметь брусок в момент соскальзывания с доски?
(10 баллов) На гладкой горизонтальной поверхности находится доска массы М и длины L. На краю доски лежит брусок массы m. К бруску приложили горизонтальную силу F такую, что брусок начал скользить по доске. Коэффициент трения между бруском и доской равен μ. Какую скорость будет иметь брусок в момент соскальзывания с доски? 

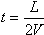 . Искомое расстояние
. Искомое расстояние 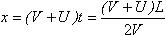 =87,5 м.
=87,5 м. 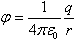
 Т.к. U>0, то U =
Т.к. U>0, то U = 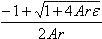
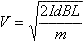 .
. 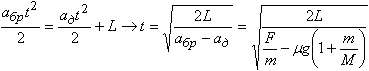
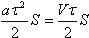 , где S — площадь сечения шланга.
, где S — площадь сечения шланга.
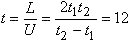 ч.
ч. 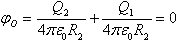 (оболочка заземлена), откуда Q2 = –Q1. Потенциал шара будет складываться из потенциала φ1, обусловленного его собственным зарядом, и потенциала φ2, обусловленного зарядом оболочки Q2 = –Q1: φ = φ1 + φ2 = φ1 (R2 – R1) / R2.
(оболочка заземлена), откуда Q2 = –Q1. Потенциал шара будет складываться из потенциала φ1, обусловленного его собственным зарядом, и потенциала φ2, обусловленного зарядом оболочки Q2 = –Q1: φ = φ1 + φ2 = φ1 (R2 – R1) / R2. 
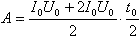 .
. 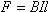 . Импульс этой силы равен импульсу, приобретенному стержнем, (V — скорость стержня в момент t). Отсюда
. Импульс этой силы равен импульсу, приобретенному стержнем, (V — скорость стержня в момент t). Отсюда  . Из закона сохранения энергии
. Из закона сохранения энергии 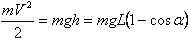 , откуда
, откуда 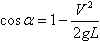 →
→  .
. 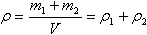 , P0 = P1 + P2. Из уравнения Клапейрона-Менделеева для давлений P1 и P2 имеем
, P0 = P1 + P2. Из уравнения Клапейрона-Менделеева для давлений P1 и P2 имеем 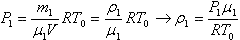 и
и  .
.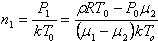 .
. 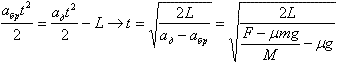 .
. 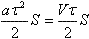 , где S — площадь сечения шланга.
, где S — площадь сечения шланга.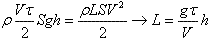
 ,
, 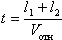
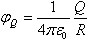 . Тогда . Отсюда
. Тогда . Отсюда 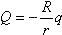 .
. 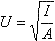 , тогда
, тогда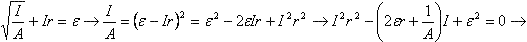
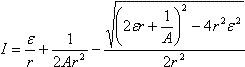 .
. 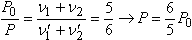 .
. 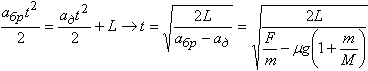 → V = aбрt.
→ V = aбрt. 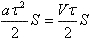 , где S — площадь сечения шланга.
, где S — площадь сечения шланга.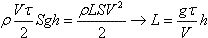
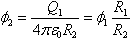 .
. 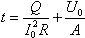 .
. 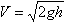 . Отсюда
. Отсюда 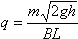 .
. 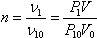 .
.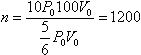 .
.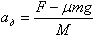 и aбр = μg. К моменту соскальзывания бруска t выполняется условие
и aбр = μg. К моменту соскальзывания бруска t выполняется условие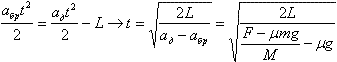 .
.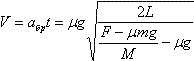 .
. 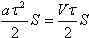 , где S — площадь сечения шланга.
, где S — площадь сечения шланга.